Let’s say have a hospital manager and you are short-staffed on doctors. Because you are short-staffed you can’t just take care of all the patients immediately. You have to triage. What you need to do is when a patient comes, asses their status and give them a priority number associated with the severness of their case. What you need is a priority queue!

Unlike its cousin, the queue, a priority queue doesn’t follow the First In First Out (FIFO) logic, the priority queue sorts items based on their priority value.

But how can we do that? There are many ways to implement such a queue but the two most common ones are a linked list and a heap.

Linked List

A linked list is a linear data structure in which elements, called nodes, are stored sequentially. Unlike arrays, where elements are stored in contiguous memory locations, linked list elements are not necessarily adjacent in memory. Instead, each element contains a reference, often called a pointer or a link, to the next element in the sequence. This arrangement allows for dynamic memory allocation and efficient insertion and deletion operations at any position within the list.

Anatomy of a linked list

The linked list consists of 3 elements:

  • node
  • head
  • tail

A node represents each element inside a linked list. It usually consists of two parts the data, which stores the actual value, and a pointer to the next node of the sequence.

The head is the first node of the linked list and serves as the starting point of the list.

The tail is the last node of the linked list and its next points to null indicating the end of the list.

Types of linked lists

A linked list can be categorized into three types based on their structure:

  • Singly linked list where each node only contains the data and the pointer to the next node. Traversal of the list can only be done in one direction, starting from the head and proceeding towards the tail.
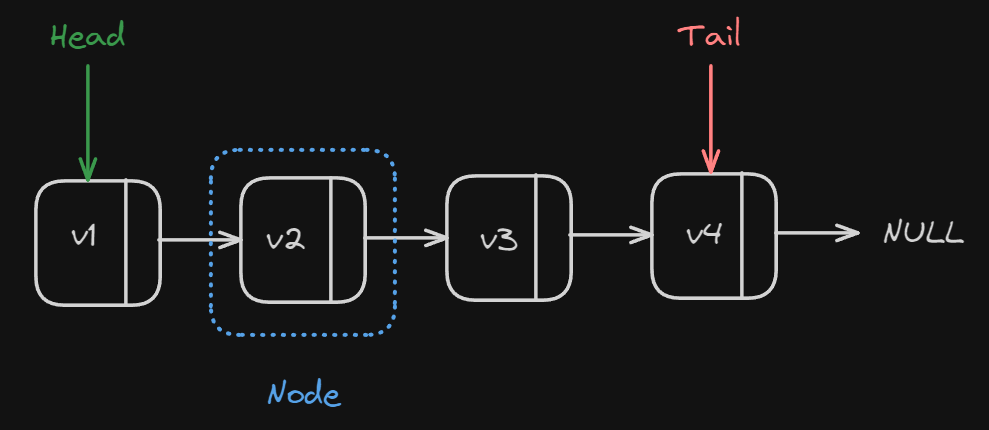
singly_linked_list

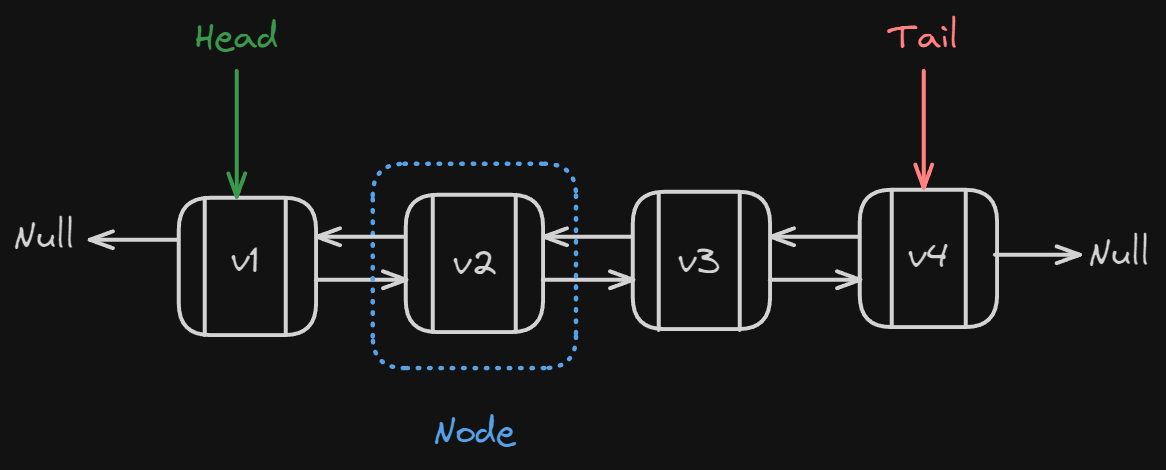
  • Doubly linked list where each node contains two references, one that points to the next node and one that points to the previous. This allows traversal in both directions. dubly_linked_list

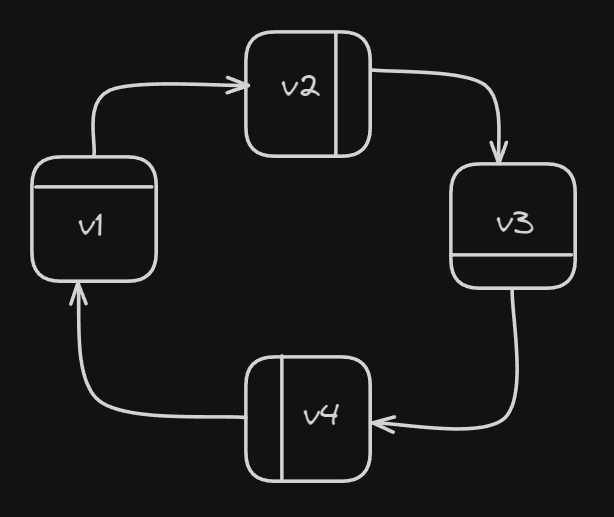
  • Circular linked list where the last node points back to the head, forming a circular structure. This eliminates a distinct head and tail. Transversal in this case is continuous. circular_list

Heap

A heap is a specialized tree-based data structure that satisfies something called the heap property. A very common heap type, and the one we will discuss today is a binary tree, but other types of heaps exist. Heap allows high efficiency and logarithmic growth.

Anatomy of a binary heap

The key characteristics of a heap are:

  • Heap property, actually is what distinguishes a binary tree from a heap. there are two types of heaps, a min heap and a max heap. For a tree to satisfy this tree proposes. For example in a max heap for any node other than the root, the value of this node must be greater or equal to the values of its children. In a min heap, it’s the opposite where the node must be less than or equal to the children

Here is an example of a min-heap:

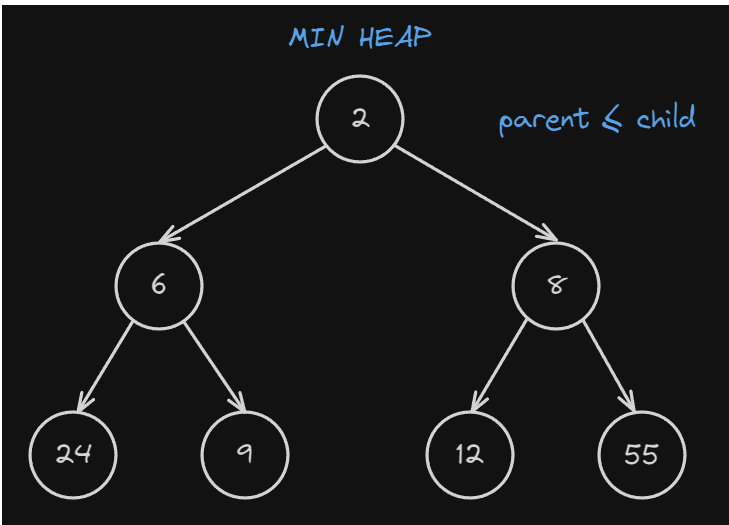
min_heap

As you can see, to satisfy the min-heap property the parent must always be less or equal to the child

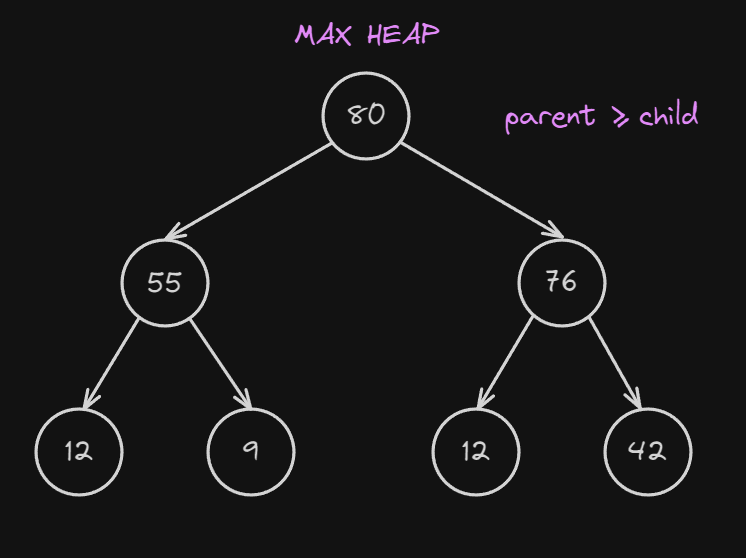
Here is an example of a max-heap: max_heap

As you can see, to satisfy the max-heap property the parent must always be more or equal to the child

  • Shape Property: A binary heap is a complete binary tree, which means that all levels of the tree, except possibly the last one, are filled, and if the level is not full, it is filled from left to right.

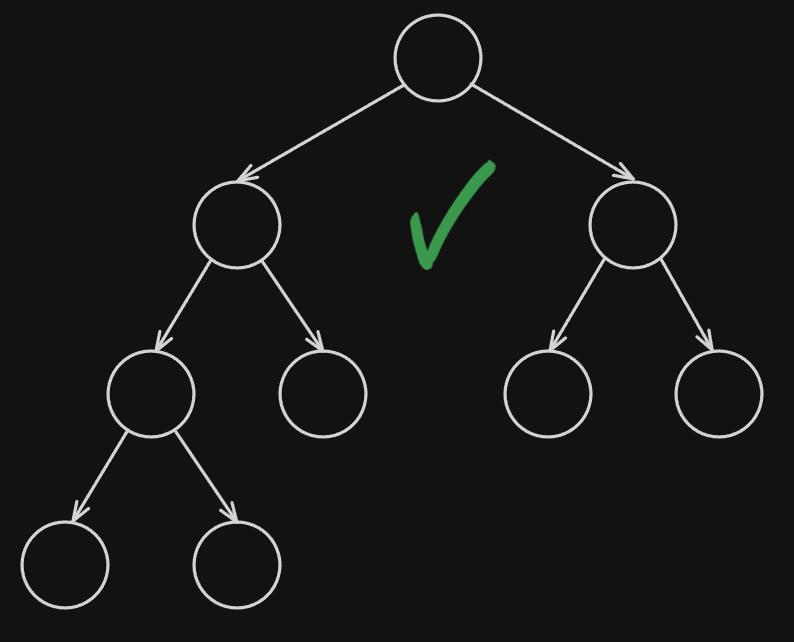
This means that to be considered a complete primary tree the nodes must be filled from left to right:

In this image we have a complete binary tree, even though it’s not full, the child nodes are filled from left to right so this tree is complete. correct_tree

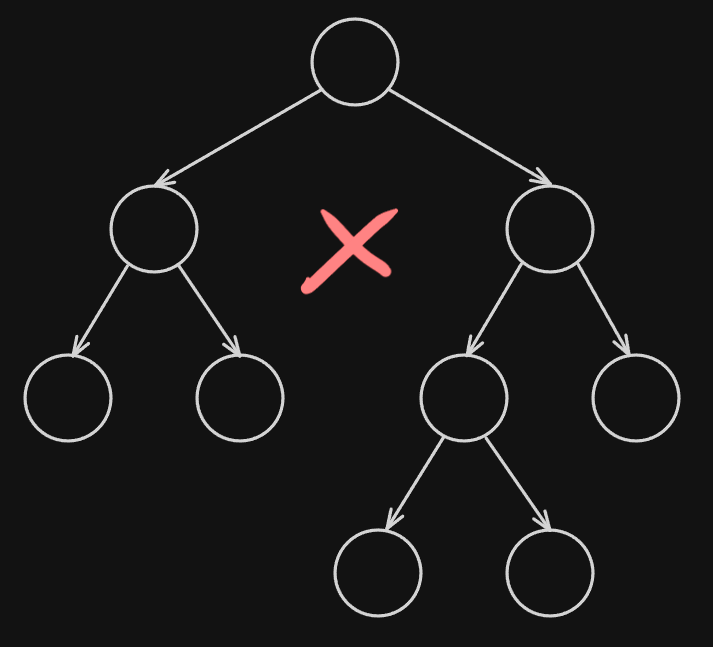
This image doesn’t have a complete binary tree, because we can see that, going from left to right, the first two nodes don’t have children and only the third one has wrong_tree

Inserting values into the heap

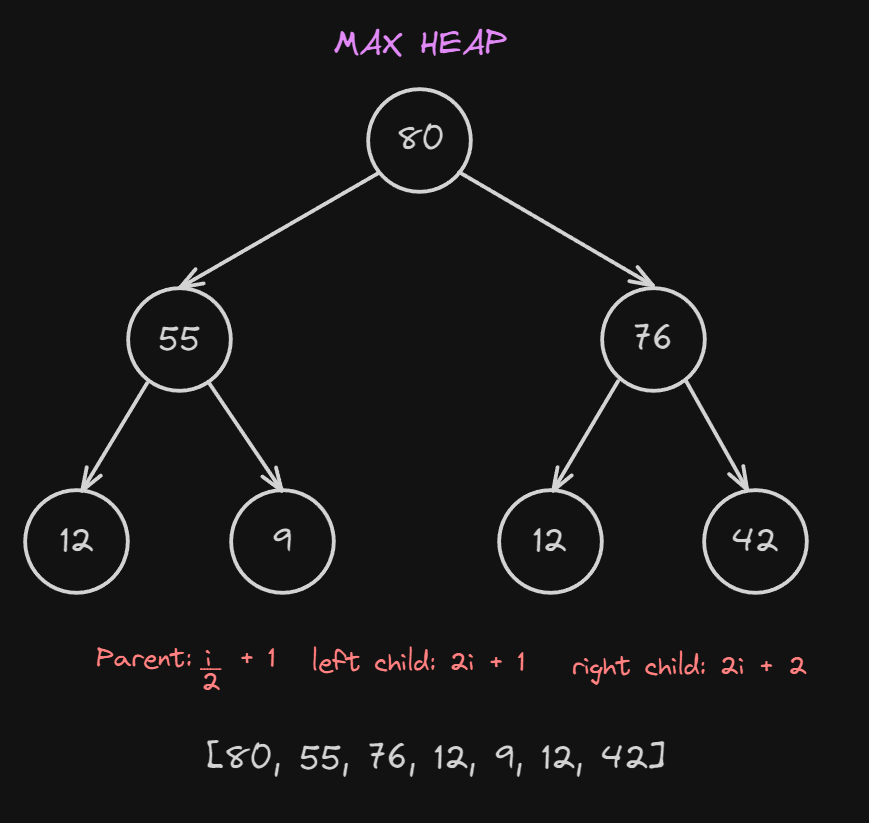
To understand how to insert values inside our heap we first need to see how to store a heap structure inside a list:

To do that we simply insert each value of the heap from left to right and from top to bottom inside a list.

Then to calculate who the child and who is the parent of a specific node we use these 3 formulas:

  • To find the parent: $\frac{i}{2} - 1$
  • To find the left child: $2i + 1$
  • To find the right child: $2i + 2$

NOTE: $i$ is the index of the list, and the list is indexed at 0.

heap_in_a_list

Now that we understand how we can represent a heap inside a list we can talk about inserting values inside.

inset a new value inside the heap we must remember the rule, always fill from left to right, by following this rule we can append our value $100$ inside our list and in our heap, it’s represented as the left child of $12$.

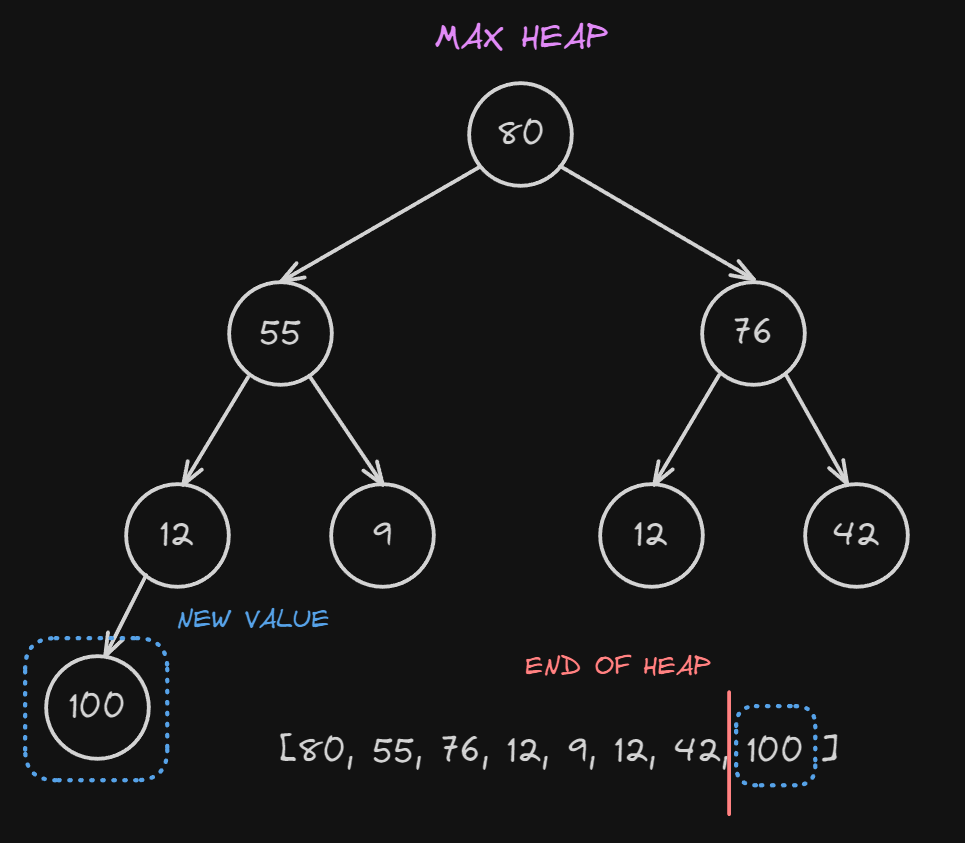heap_in_a_list At this point, we have successfully appended our node to our heap, but there is a problem! We just broke the max heap property.

To fix it we need to perform a function called heapify, more specifically we heapifing up.

To do this what we do is pretty simple:

  • compare the parent
  • if the parent is smaller than the child, swapp them
  • reaped until this condition is no longer true or we have reached the root

Let’s look at an example:

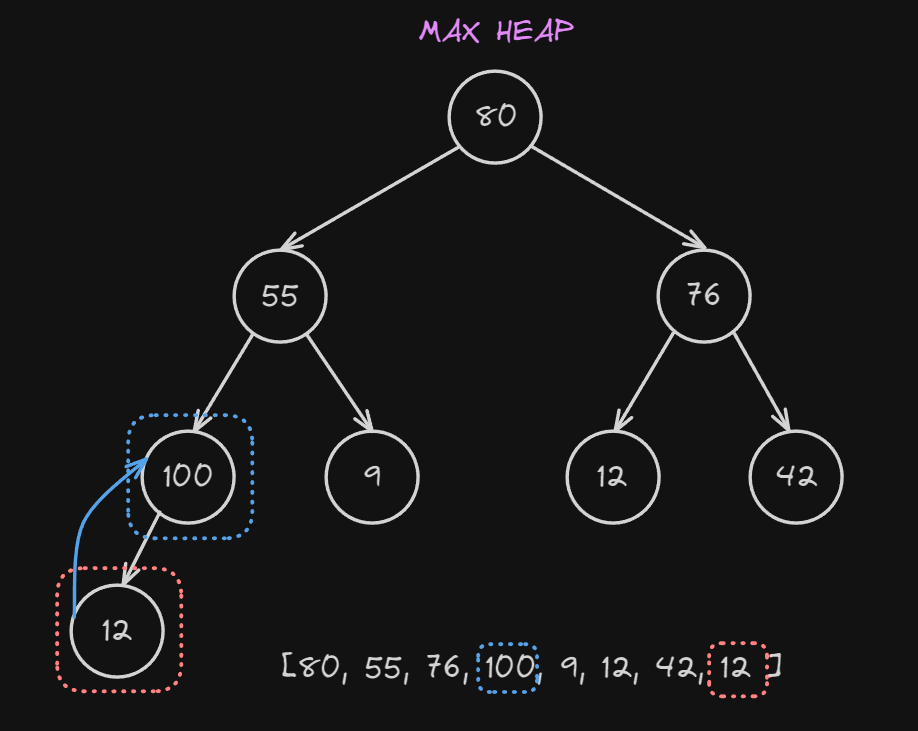
first_step_heapify

We have added the value $100$ to our list, we now compare it with the parent node $12$, because $100 > 12$ we swap them.

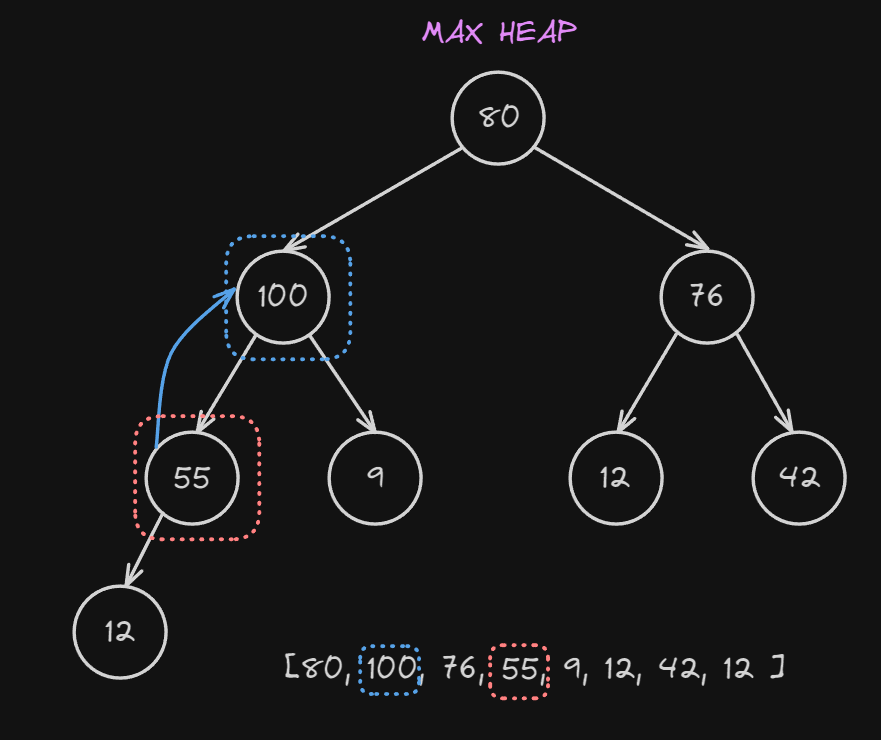
We now compare again the node $100$ with its new parent $55$, also in this case $100 > 55$ so we swap again. second_step_heapify

Finally, we compare one last time and again $100 > 80$ so we swap one last time.

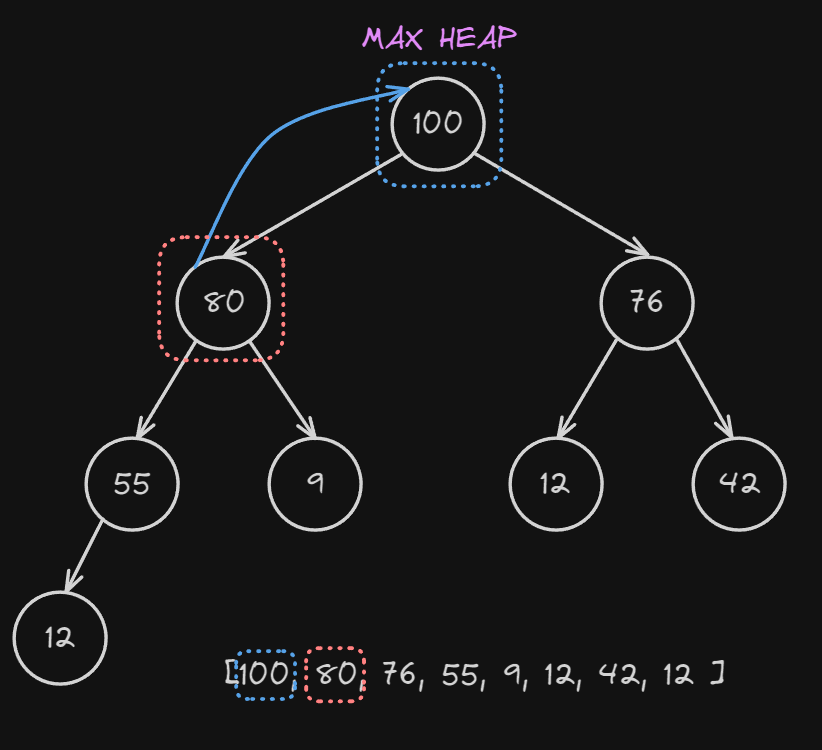
third_step_heapify

At this point, we have successfully heapified our list!

Deleting values from the heap

To delete values from our heap and still maintain the heap properly we can only delete the root of the heap.

Ok, easy enough, but now what do we put at the root of the heap?

We know for a fact that we can only remove elements by doing the inverse of insertion. We can remove elements from the heap from the bottom up and from right to left.

Take as an example this heap:

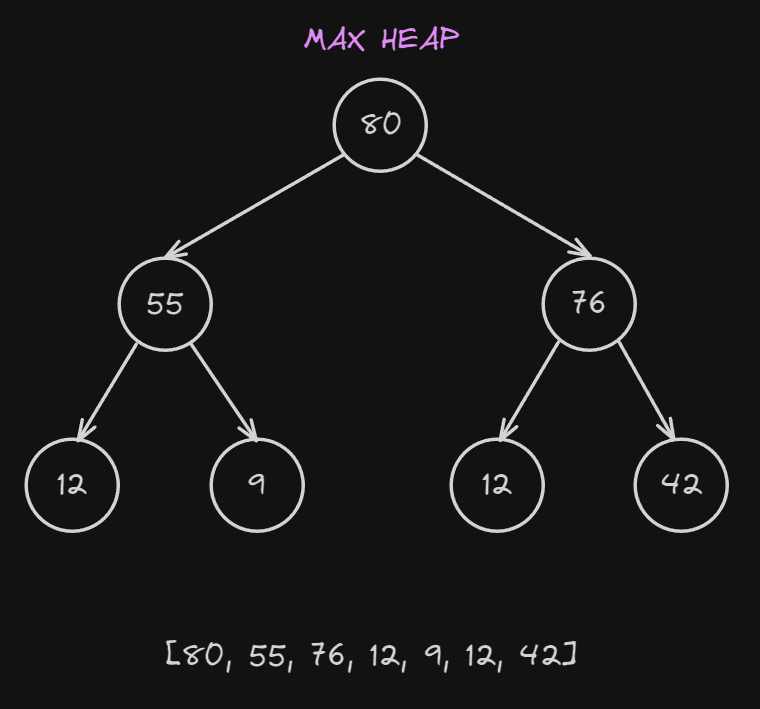
remove_first_phase

We remove the root, which is $80$ and we put in its place the last element of the heap which is $42$.

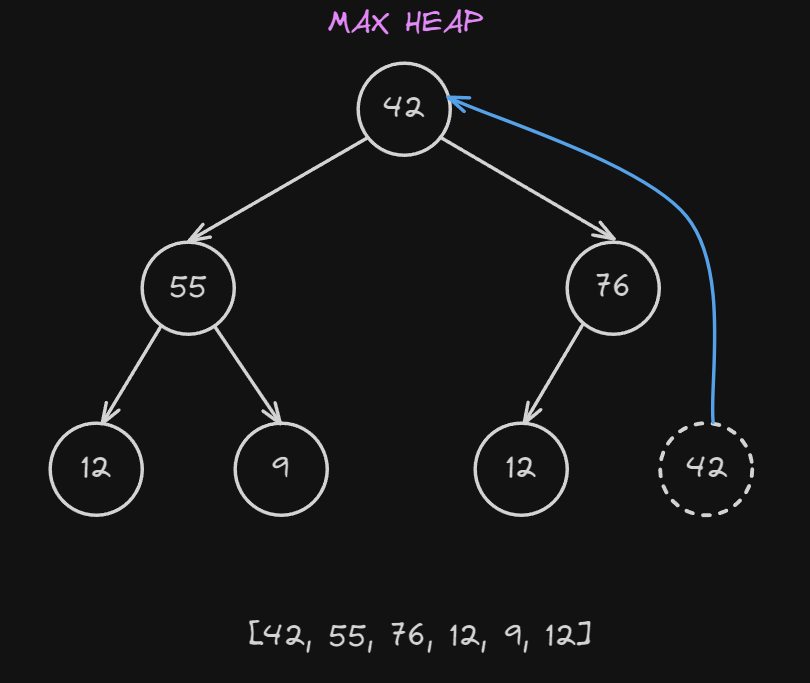remove_second_phase At this point, we have successfully removed the root of the heap and replaced the root node while keeping a complete binary tree structure. But, by doing this we have broken our heap property.

To fix this we need to perform again a heapify function but this time we need to heapify down.

To do this we need to:

  • check which of the two children is the biggest
  • check if the biggest child is bigger than the parent
  • if the parent is bigger swap them places In this example, we have two children $55$ and $76$ so out of the two $76 > 55$ so the left child is the biggest one.
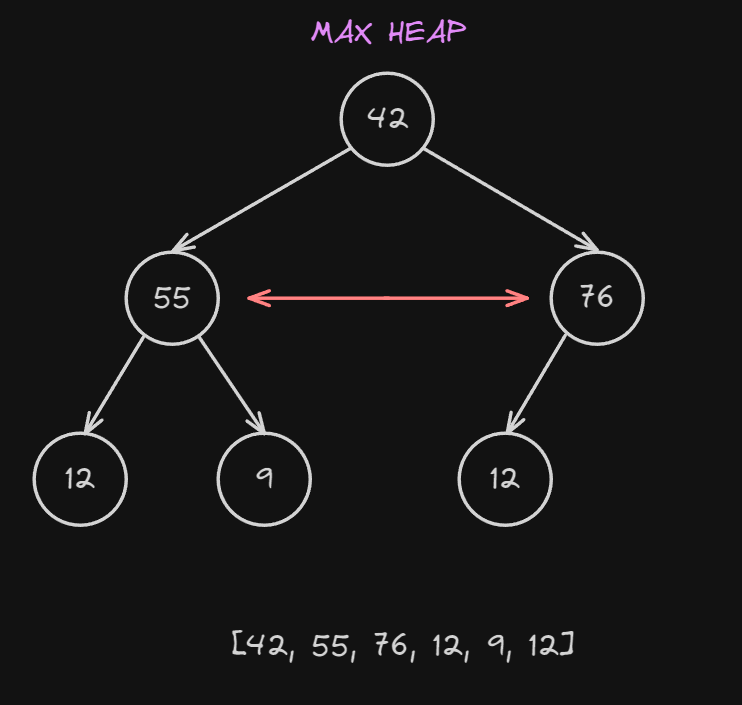
remove_fourth_phase

Now, we check if the parent $42$ is bigger than $76$, which it is so we swap them

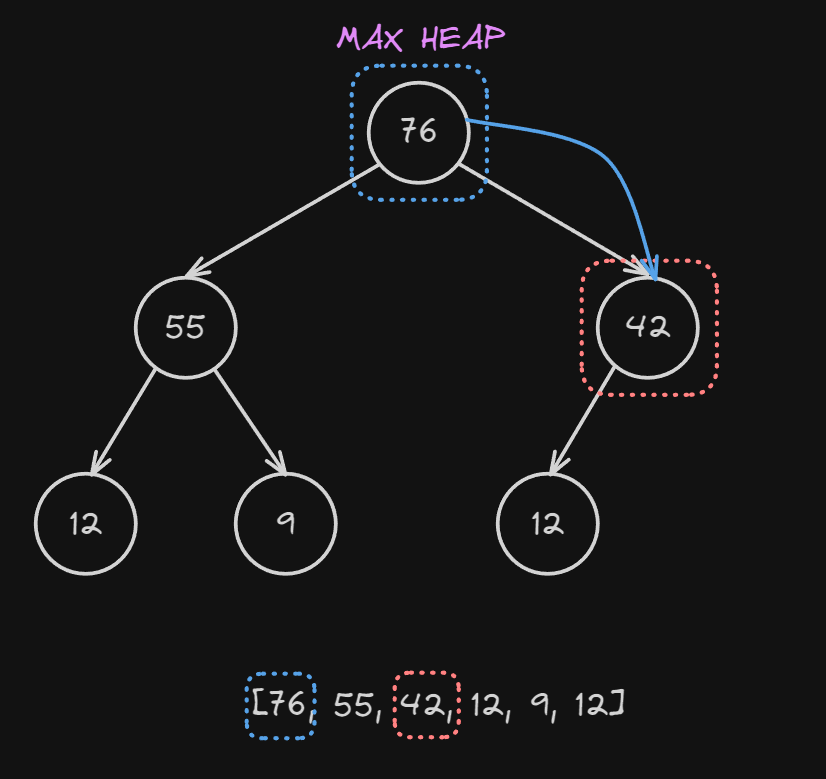
remove_fifth_phase

At this point we check again the children of $42$, in this example, there is only one child so we can skip the step. Now we check if $42 > 12$ which is true so we don’t need to swap the parent with the child.

This means that the max heap condition is now met and we have successfully removed a value from the heap.

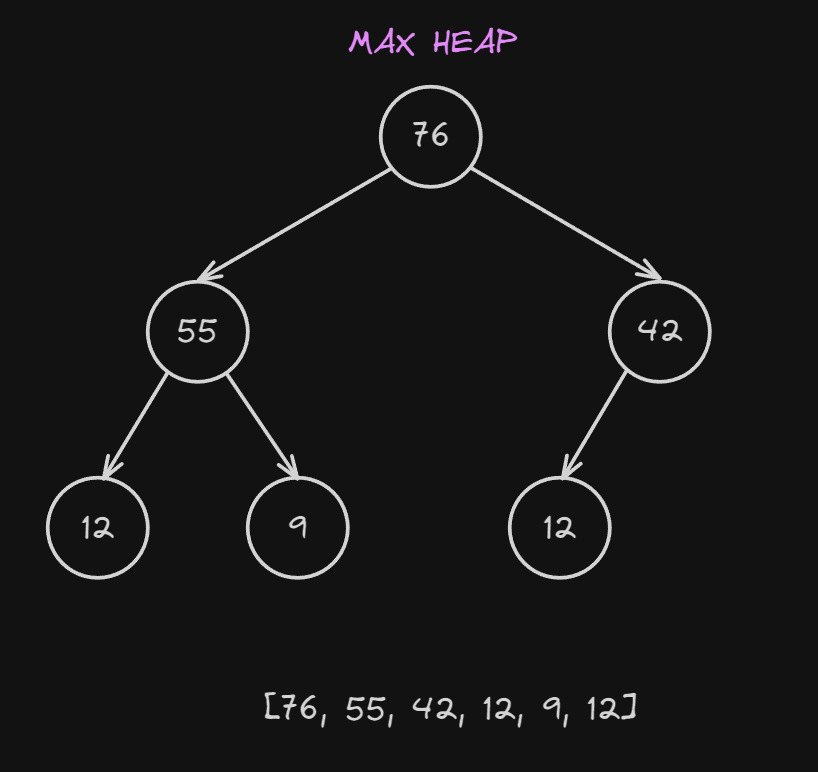
Our heap will now look like this! remove_sixth_phase

Choosing a heap over a linked list

When implementing a priority queue there are several advantages to using a heap rather than a linked list. Most notable is their efficiency.

Heaps provide efficient insertion and deletion of elements, both of which are common operations in a priority queue. In particular, heaps support insertions and deletions in $O(\log n)$ time complexity, where n is the number of elements in the heap. Linked lists, on the other hand, may require $O(n)$ time complexity for insertion and deletion operations, especially when you need to maintain the list in sorted order. With heaps, you are dealing with logarithmic complexity while with a linked list you are dealing with linear complexity.

Another point toward the heap is that heaps maintain the priority property efficiently, ensuring that the element with the highest priority (or lowest priority, depending on whether it’s a max-heap or min-heap) is always at the root. This property simplifies the implementation of priority queues, as you don’t need to manage the order of elements manually.

Implementing heap in Python

To implement a heap in Python we need a couple of methods, more specifically we need:

  • a method to find the parent
  • a method to find the right child
  • a method to find the left child
  • a method that swaps two elements
  • a method that adds items to the heap
  • a method that heapifies up
  • a method that removes items from the heap
  • a method that heapifies down
  • a method that returns the smallest child
class PriorityQueue:
    def __init__(self):
        self.heap = []
    
    def __repr__(self):
        return repr(self.heap)
    
    def parent(self, index):
        return (index - 1) // 2
    
    def left_child(self, index):
        return 2 * index  + 1

    def right_child(self, index):
        return 2 * index  + 2
    
    def swap(self, i, j):
        self.heap[i], self.heap[j] = self.heap[j], self.heap[i]

    def is_empty(self):
        return len(self.heap) == 0

The first method is the contractor, which runs every time the class gets instantiated.

The __repr__ method is a special method that returns the string representation of an object

The parent returns the parent of a node based on its index, and so do the left_child and right_child methods.

The swap method swaps the nodes.

The is_empty method checks if the length of the heap is $0$ and returns True or False based on that.

    def enqueue(self, item, priority):
        self.heap.append((item, priority))
        self.heapify_up(len(self.heap) - 1)
    
    def heapify_up(self, index):
        while index > 0 and self.heap[index][1] < self.heap[self.parent(index)][1]:
            self.swap(index, self.parent(index))
            index = self.parent(index)

The enqueue method appends a new node inside the heap and then calls the heapify_up function to maintain the min-heap property.

The heapify_up method calls the swap method, while the index is more than 0, because index 0 is the root of the heap, and the parent of our node is bigger than it. NOTE: this time we are implementing a min-heap At the end it sets the parent of the node to the node itself so that in the next pass, we can check the new parent.

    def dequeue(self):
        if self.is_empty():
            raise IndexError("Queue is empty")
        self.swap(0, len(self.heap) - 1)
        item = self.heap.pop()[0]
        self.heapify_down(0)
        return item

The dequeue method removes the root of the item in the heap unless the queue is empty, in that case, it raises an IndexError.

Then it calls the swap method, to swap the root of the heap with the last element. After that, the function calls the self.heap.pop()[0] to remove the last element of our list (which is the previous root, before the swap).

Then the method calls the heapify_down method to maintain the heap condition, and at the end, it returns the deleted item.


    def heapify_down(self, index):
        while self.left_child(index) < len(self.heap):
            smallest_child = self.get_smallest_child(index)
            if self.heap[index][1] > self.heap[smallest_child][1]:
                self.swap(index, smallest_child)
                index = smallest_child
            else:
                break

In the heapify_down method, a while loop is instantiated that continues as long as the index of the left child of the current node is within the bounds of the heap. This condition ensures that the loop will terminate when the current node has no left child, indicating it’s a leaf node.

Then it calls the smallest_child method to get which one of the two children is the smallest, and then checks if the child is bigger than the node.

If this condition is true the swap method is called to swap them places and finally set the index to the smallest child so that we can traverse down the heap.

    def get_smallest_child(self, index):
        left_child_index = self.left_child(index)
        right_child_index = self.right_child(index)

        if right_child_index < len(self.heap) and self.heap[right_child_index][1] < self.heap[left_child_index][1]:
            return right_child_index
        else:
            return left_child_index

In the get_smallest_child method it gets, the two children values by calling the left_child and right_child methods.

If the index of the right child is within the bounds of the heap and if the priority of the item at the right child index is less than the priority of the item at the left child index. This condition determines if the right child is smaller than the left child. If the condition is True then it returns the right child else it will return the left child.

Complete code implementation

class PriorityQueue:
    def __init__(self):
        self.heap = []
    
    def __repr__(self):
        return repr(self.heap)
    
    def parent(self, index):
        return (index - 1) // 2
    
    def left_child(self, index):
        return 2 * index  + 1

    def right_child(self, index):
        return 2 * index  + 2
    
    
    def swap(self, i, j):
        self.heap[i], self.heap[j] = self.heap[j], self.heap[i]

    
    def enqueue(self, item, priority):
        self.heap.append((item, priority))
        self.heapify_up(len(self.heap) - 1)
    
    def heapify_up(self, index):
        while index > 0 and self.heap[index][1] < self.heap[self.parent(index)][1]:
            self.swap(index, self.parent(index))
            index = self.parent(index)
        
    
    def dequeue(self):
        if self.is_empty():
            raise IndexError("Queue is empty")
            return self.heap[0][0]
        self.swap(0, len(self.heap) - 1)
        item = self.heap.pop()[0]
        self.heapify_down(0)
        return item

    

    def heapify_down(self, index):
        while self.left_child(index) < len(self.heap):
            smallest_child = self.get_smallest_child(index)
            if self.heap[index][1] > self.heap[smallest_child][1]:
                self.swap(index, smallest_child)
                index = smallest_child
            else:
                break

    def get_smallest_child(self, index):
        left_child_index = self.left_child(index)
        right_child_index = self.right_child(index)

        if right_child_index < len(self.heap) and self.heap[right_child_index][1] < self.heap[left_child_index][1]:
            return right_child_index
        else:
            return left_child_index
        
    
    def is_empty(self):
        return len(self.heap) == 0
``