17 minutes
Using The Minimax Algorithm For Tic Tac Toe
This week in my uni I was tasked to create a simple tic-tac-toe application in Python so that we can familiarize ourselves with the notion of two-dimensional arrays and OOP in Python.
Creating the board itself was very simple alongside the method for displaying the array was easy.
Making the tic-tac-toe game in Python
class TicTacToe:
def __init__(self) -> None:
self.board = [
['-', '-', '-'],
['-', '-', '-'],
['-', '-', '-']
]
def display_board(self):
for i in range(3):
for j in range(3):
print(self.board[i][j], end=' ')
print()
The next step of this application was creating a method for letting the human play.
def human_play(self, player):
while True:
row = int(input("Row: "))
col = int(input("Col: "))
if row < 0 or row > 2 or col < 0 or col > 2:
print("Wrong row or col")
elif self.board[row][col] == '-':
self.board[row][col] = player
return row, col
else:
print("Error, position is occupied")
This simple function simply prompts the users for the x and y coordinates inside the 3X3 Matrix that is the tic-tac-toe board. I understand that playing while keeping in mind that arrays are indexed 0 is not the most gamer-friendly approach but the focus of this exercise was implementing the minimax algorithm.
Before we can start implementing the algorithm we must first fulfill a couple of pre-requisites:
- make a method that gets the winner
- make a method that sees if there is a tie
Let’s start with making a function that finds a winner.
def is_winner(self, player):
for i in range(3):
if all(self.board[i][j] == player for j in range(3)) or all(self.board[j][i] == player for j in range(3)):
return True
if all(self.board[i][i] == player for i in range(3)) or all(self.board[i][2 - i] == player for i in range(3)):
return True
return False
This method has two if statements.
The first one is responsible for finding horizontal and vertical wins.
Let’s break this if statement in two so that we can have a better understanding of what’s going on.
for i in range(3):
if all(self.board[i][j] == player for j in range(3)):
return True
This first part checks if all the elements inside the specific row i are equal to the specific player’s symbol.
for j in range(3) loops inside each column inside the i row.
self.board[i][j] == player checks if the element is comparatively equal to the player’s symbol and if it’s true it returns True.
The all() function takes an iterable (in this case, a generator expression) and if all the values return True then it also returns true.
The same is later done in the second part of this if statement but the self.board[i][j] become self.board[j][i] so that it scans vertically
instead of horizontally.
The second if statement functions essentially the same as the first one but this time it loops only a single time and i is put
inside both idices self.board[i][i] == player for i in range(3) to get the first diagonal.
The second diagonal a negative number is used to wrap the index at the beginning of the list.
The last piece of the puzzle before getting into the algorithm is finding when a tie occurs. To do that we can simply check if the board is full, and if it is and no winner is found that means we have a draw in our hands.
def is_board_full(self):
for i in range(3):
for j in range(3):
if self.board[i][j] == '-':
return False
return True
The implementation is pretty simple we just check if a space exists "-" if there is, then the loop breaks returning false
meaning that the board is not full yet.
The Algorithm
Before showing the implementation it is important to understand how the minimax algorithm works.
The minimax algorithm is a backtracking algorithm used in game theory for finding the optimal move in a turn-based game assuming optimal play. The algorithm has two players, the maximizer and the minimizer. The maximizer tries to get the highest score possible while the minimizer tries the opposite.
Every board has a state associated with a value, the maximizer tries to move the game toward a game state with the highest score possible.
The game state is represented as a decision tree where each corresponds to a possible game position. The root of the tree represents the current game state, and each child node (branch) represents a possible move.
To have a better idea of this tree I drew up a tic-tac-toe example. The reason why the root of this example is mid-game is because tic-tac-toe has 9 tiles making the possible combinations of the tree 9! which is equal to 362880. Way too many combinations for me to draw lol.
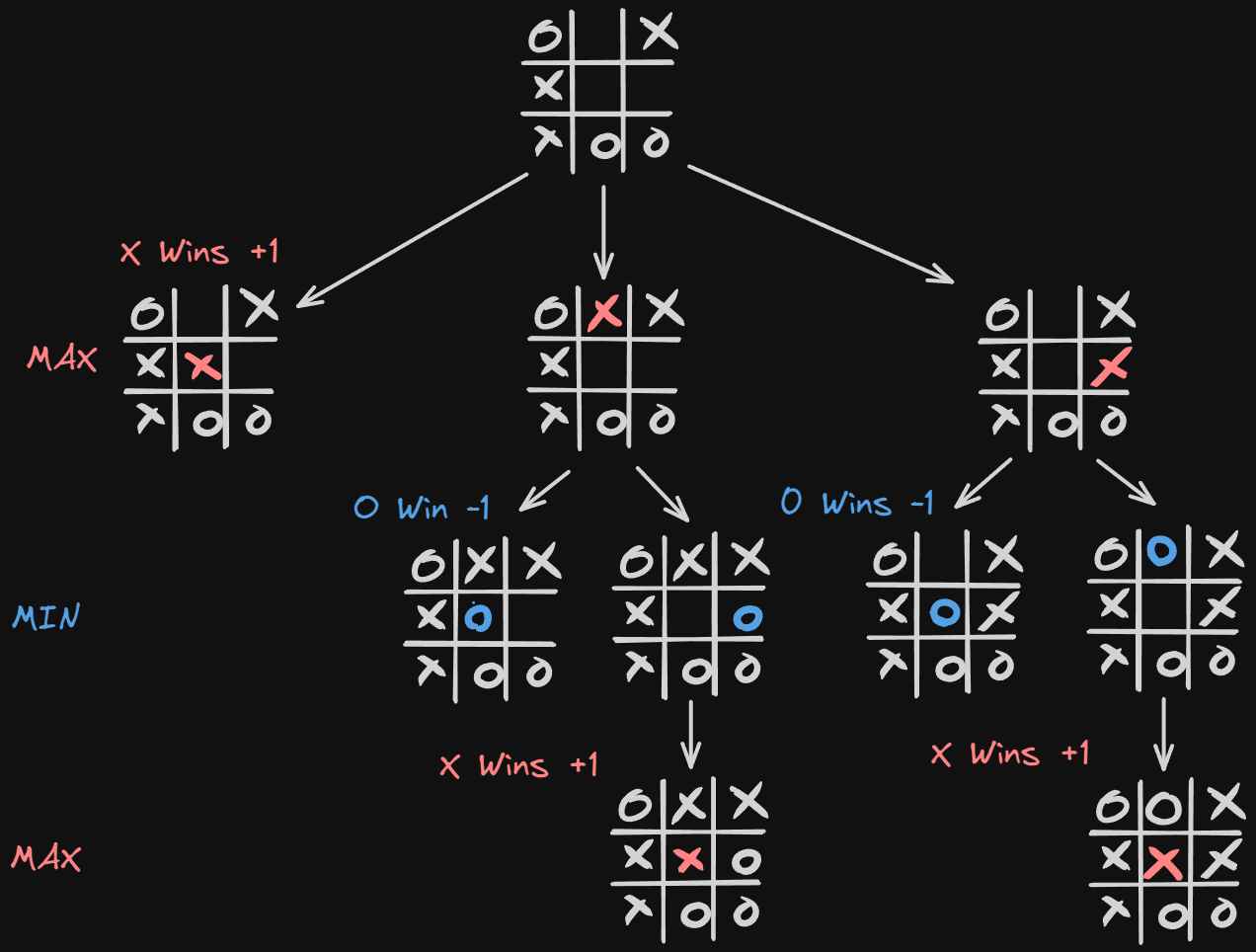
To algorithm recursively expands the game tree, considering all moves for both players, up to a certain depth (because tic-tac-toe is a simple game the computer always reaches the terminal state (win, lose, draw)).
At the leaf node of the terminal state (the end of the tree), an evaluation function is applied to determine if the outcome is desirable for the current user. Since tic-tac-toe is simple our function can simply be:
- win = + 1
- lose = - 1
- draw = 0
The evaluation score then gets propagated back up the root of the tree, alternating between maximizing and minimizing players. The maximizing player will try to maximize the score by choosing a decision that maximizes the evaluation score whilst the minimizing player will try to minimize the score.
Once the tree is evaluated, the algorithm selects the move that leads to the highest score or the lowest score depending on the player.
Let’s look at our example image.
After the tree’s root, it’s the maximizing player’s turn to play. In this case, it can make 3 moves. The first one grants it an immediate victory, setting the evaluation function to +1, while the second and third ones are not terminal states (win, lose, draw).
Now it’s the minimizer’s turn.
Since one outcome was terminal, the minimizing player can only go after the other 2 states. Each of these states has two child nodes. In both cases, the left node led to the minimizing player’s victory so the evaluation function is set to -1.
Now let’s look in depth at how the algorithm chooses the best move.
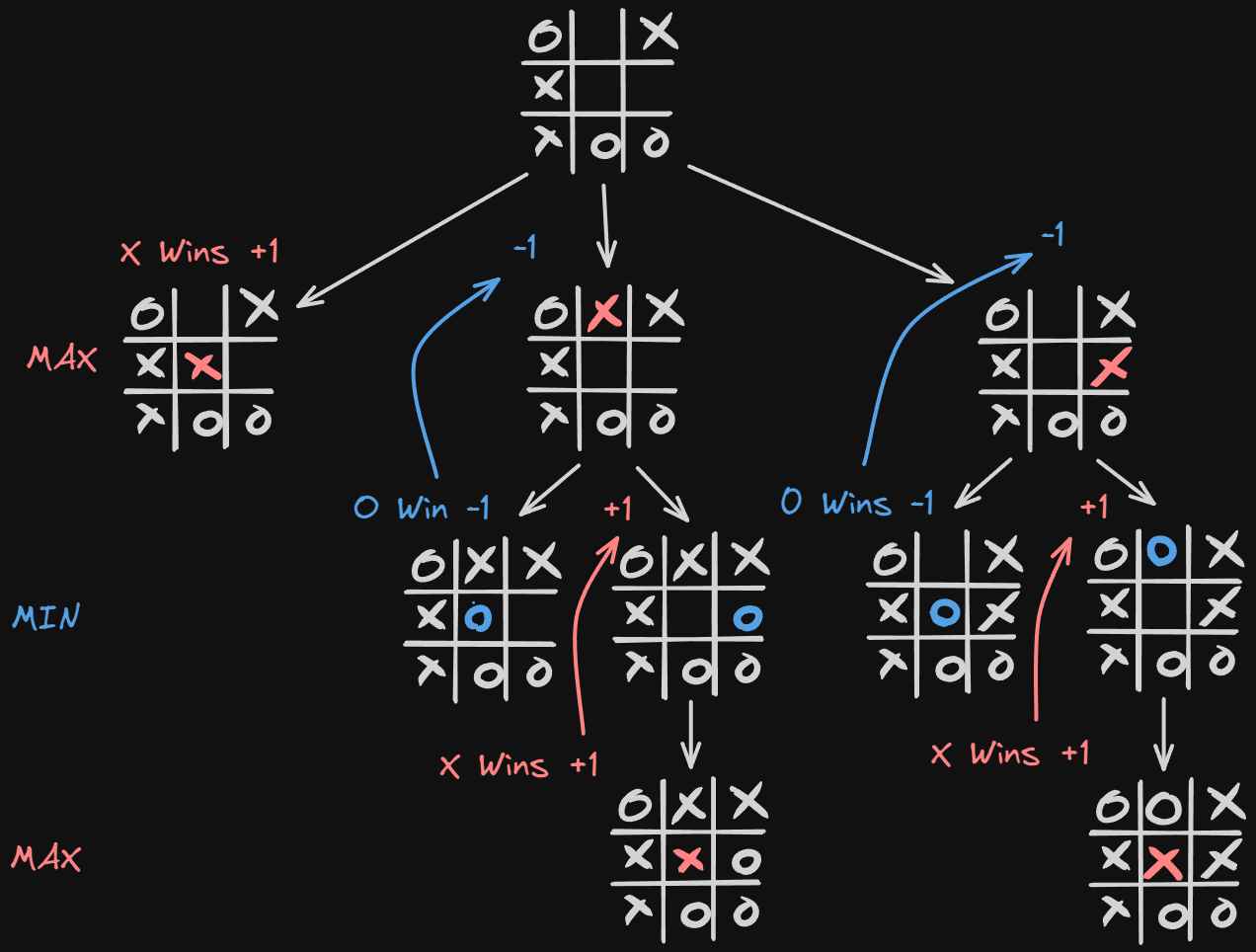
Because this algorithm assumes optimal play, this means both players always make the best decision given their current position, this means that we can deduce the evaluation score before reaching a terminal state.
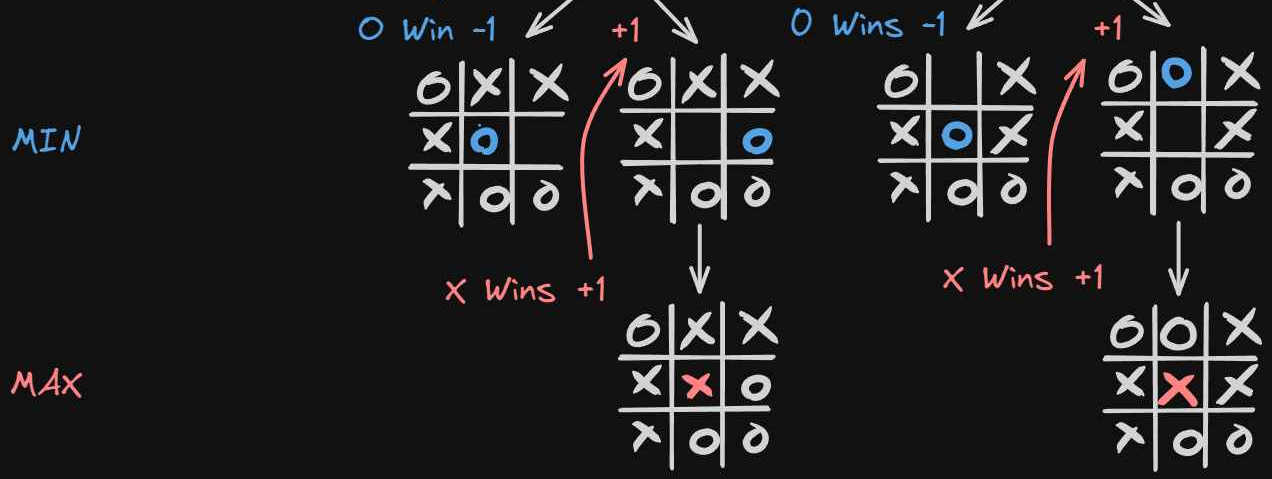
More specifically we know that if it’s the minimizer’s turn, then it can make two plays. One will lead it to victory and the other one will not be a terminal state. But because after the minimizer’s turn, it’s the maximizing player’s turn, they only have one option leading them to victory.
This means that we can assume that choosing the left option in both cases will lead to the minimizer player’s loss.
This essentially means that we can take the +1 state that we get at the end and bring it back to the nonterminal state.
Now let’s look at the next layer up so we see how the maximizing player behaves.
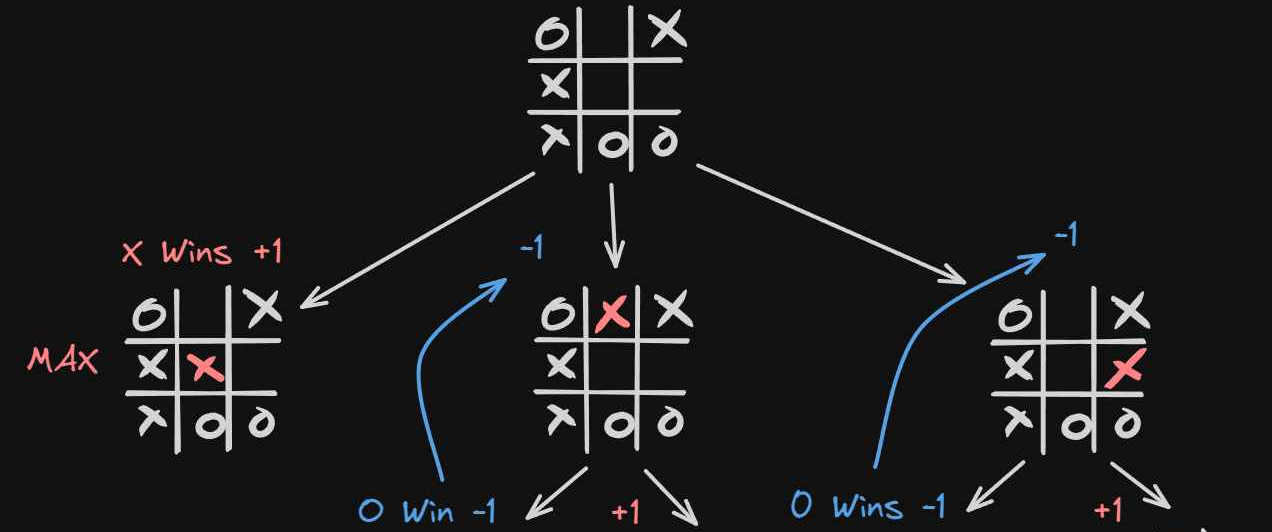
This time it’s the maximizing player’s turn, and it has 3 choices.
It can either win immediately (+1) or have 2 nonterminal states.
Because the algorithm always assumes optimal play we know, given the change between -1 and +1 the minimizing player will always
choose the play that gets them the lowest score.
In essence, this means that out of the three choices one will grant the maximizing player the +1 and the other nonterminal states will become
-1 because after its turn the minimizing player has the opportunity to get the -1 and minimize the score.
This means that the maximizing player will choose the first option that has an evaluation function = +1.
Implementing it in code
It’s finally time to implement this theory into code.
First things first, let’s make an evaluation function.
def evaluate(self):
if self.is_winner("O"):
return 1
elif self.is_winner("X"):
return -1
elif self.is_board_full():
return 0
else:
return None
As already mentioned tic-tac-toe is a very easy game to make an evaluation function.
Now let’s implement the minimax algorithm.
def minimax(self, depth, max_player):
score = self.evaluate()
if score is not None:
return score
if max_player:
max_value = -2
for i in range(3):
for j in range(3):
if self.board[i][j] == '-':
self.board[i][j] = 'O'
eval = self.minimax(depth + 1, False)
self.board[i][j] = '-'
max_value = max(max_value, eval)
return max_value
else:
min_value = 2
for i in range(3):
for j in range(3):
if self.board[i][j] == '-':
self.board[i][j] = 'X'
eval = self.minimax(depth + 1, True)
self.board[i][j] = "-"
min_value = min(min_value, eval)
return min_value
The first thing this method does is evaluate the score.
By looking at the evaluation method we can see that unless we reach a terminal state the
method will return None, in the minimax function we check if we have reached a terminal state, and if so
we return the score.
The algorithm revolves around two players, and so we have a big if statement.
If max_player is true, we are the maximizing player and so we must set the value at something as low as possible.
In this case, I went -2 which is lower than the lowest possible value.
Then we perform two loops to inspect the entire two-dimensional array.
If we find a free spot we place our "O" in that spot.
At this time we iterate by calling the minimax() again, increasing the depth value and changing the max_player to False.
then we turn the board back to its original state and call the max() function.
This keeps track of the maximum value encountered among the possible moves.
What we did here is call the method again but this time as the minimizing player because the maximizing player just played
their turn.
Now that the max_player variable is false, we fall into the else clause.
Similar to the maximizing player’s block, it iterates through each
empty cell on the board, places an ‘X’, recursively calls the minimax function for the next
level of the game tree with max_player set to True, and then reverts the move, keeping track of
the minimum value encountered among the possible moves.
Finally, this function returns the maximum or minimum value, depending on whether it’s the turn of the maximizing or minimizing player, respectively.
Now that we have the algorithm we need to make a function that will return the best move for that specific instance of the game tree.
def best_move(self):
best_score = float('-inf')
best_move = None
for i in range(3):
for j in range(3):
if self.board[i][j] == "-":
self.board[i][j] = "O"
move_score = self.minimax(0, False)
self.board[i][j] = '-'
if move_score > best_score:
best_move = (i, j)
best_score = move_score
return best_move
First thing we do is initialize the best_score value. Just for fun instead of the usual -2, I went with float(-inf).
Second, we initialize best_move, which is going to be our tic-tac-toe coordinates, to None.
Now we iterate through our tic-tac-toe board using the usual nested for loops.
If we find a space then we place the O value, and then we call upon the minimax()function this function will evaluate the score for the current move. TheFalse` argument indicates that this is not the maximizing player’s turn, meaning it’s the turn of the opponent.
The next line reverts the board to its original state, ensuring that the game state remains unchanged for the next iteration.
The last part of this method simply checks if the score obtained for the current move is better than the previous best score. If it is we save the specific coordinates inside the best_move variable and then update the best_score variable to the current move_score variable.
And now simply return the best_move and the algorithm is complete.
Or is it…
Implementing α-β pruning
Actually, yeah, this algorithm is complete and it works perfectly fine as is, but Minimax on its own performs a lot of extra steps that are not needed. Using α-β pruning can increase the performance of this algorithm without impacting its effectiveness.
The basic idea behind Alpha-Beta pruning is to prune branches of the search tree that cannot influence the final decision. It maintains two branches, alpha and beta, to keep track of the range of possible values for the maximizing and the minimizing player. The pruning occurs when it is determined that certain branches will not affect the final decision.
Let’s see how this algorithm works:
First things first, we must define both alpha and beta.
- Because alpha is used for the maximizing player we will give it a default value of
-∞. - Now for beta, because it’s used by the minimizing player we will give it a default value of
+∞. - We will prune the node only when alpha becomes greater than or equal to beta.
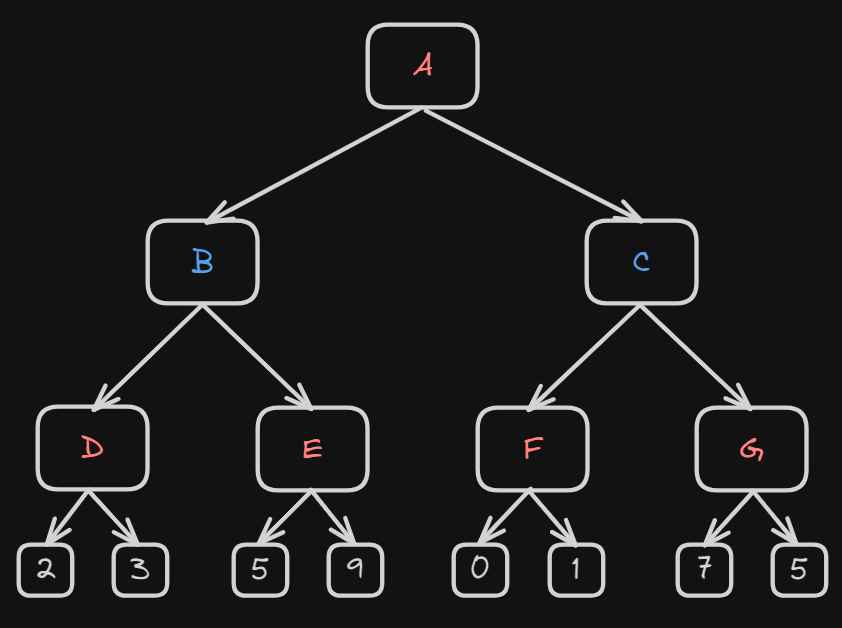
Let’s move to the first node that isn’t the root node, B. Because alpha is less than beta we don’t prune out the tree, and we move to the next turn.
Now it’s the maximizing player turn. At node D the value of alpha will be calculated
More specifically node D has two options either 2 or 3, because
it’s the maximizing player turn, they will choose option 3.
Since 3 > -∞ alpha has now become 3 and because 3 < ∞ beta will also become 3.
So at node B at this moment:
- α = -∞
- β = 3
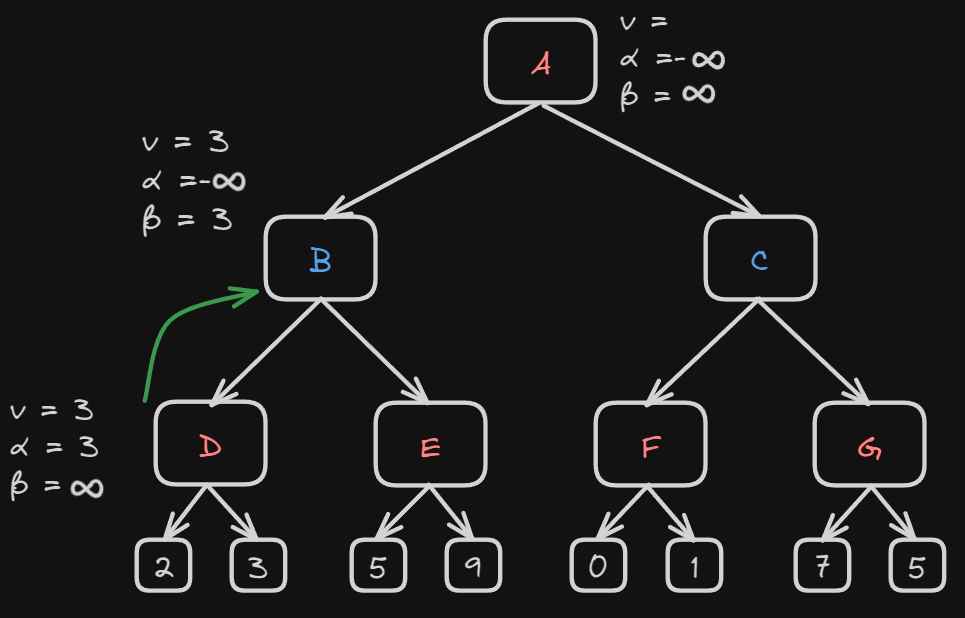
Now the minimax algorithm will traverse the next child node of B which is E.
The first value that appears under E is 5.
That means that at node E α = 5 and β = 5
This will now satisfy the condition that we can only prune when alpha becomes equal to or greater than beta.
What this means is that
At node E α = 5 and α > β so we don’t even need to compute the other outcome of the tree because in node B, when the minimizing player
is playing, they will always choose the optimal path for them (meaning the minimum number smallest number of beta) and so the game will never reach
the node E so we don’t even need to calculate the last part.
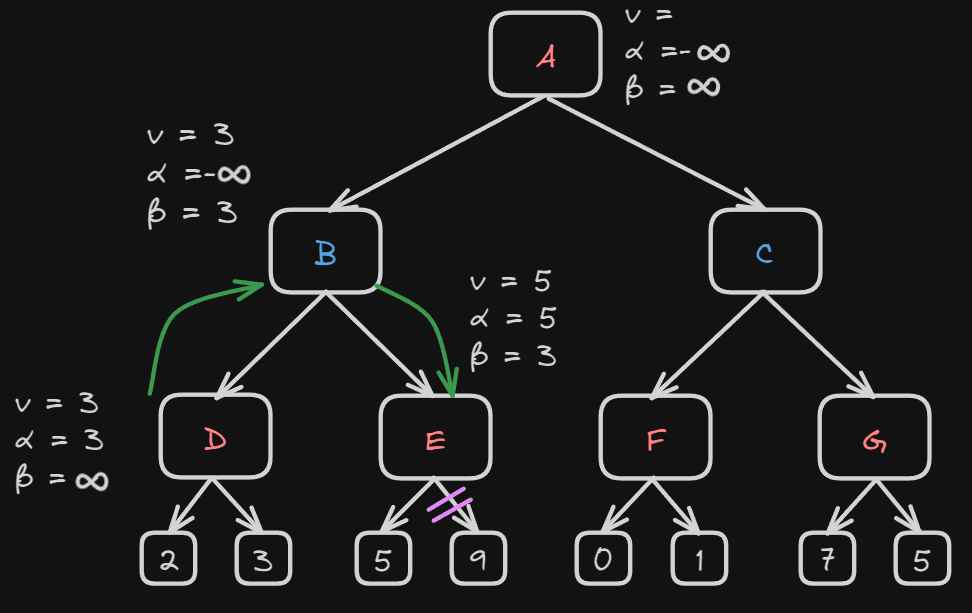
In the next step, the algorithm goes back to the node A. At node A alpha will be compared between -∞ and 3. So now alpha will become 3 and beta will be ∞.
Now the next step the algorithm will move to node C where the same values of alpha and beta will be transferred.
Now the algorithm has reached node F. Node F has values 0 and 1 because it’s the maximizer player. The return f will be 1 but alpha(3) is still bigger so it will remain unchanged.
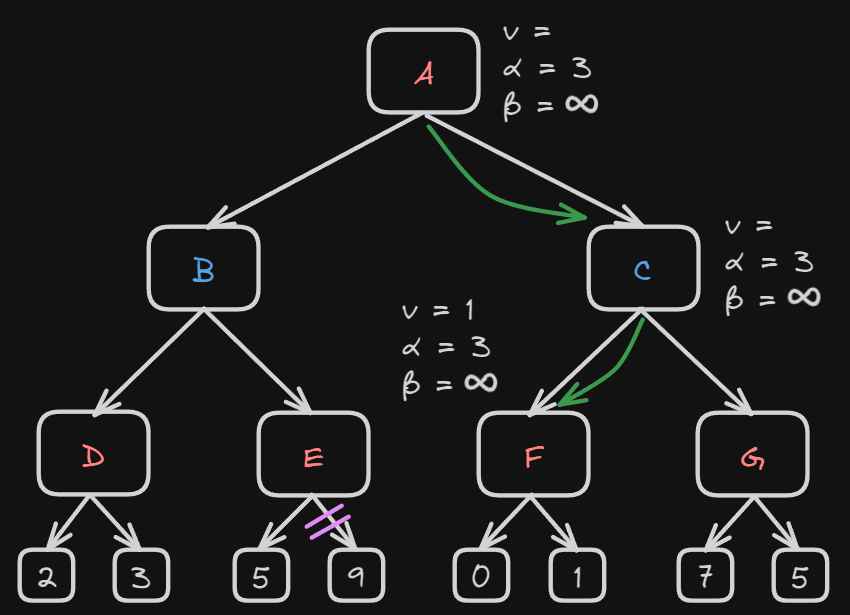
Now node F will return the node value 1 to C and will compare to the beta value at C. Now it’s the minimizer players’ turn. So beta will be compared between +∞ and 1. So now at node C:
- alpha = 3
- beta = 1
Because alpha is greater than beta, this satisfies the pruning condition so the rest of the tree can be pruned
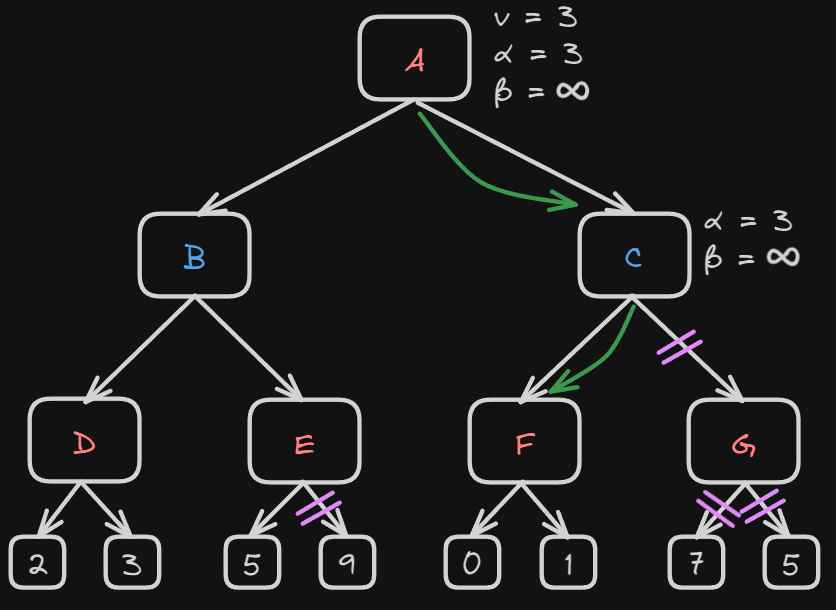
Now, C will return the node value to A and the best value of A will be between 1 and 3 so alpha will remain 3.
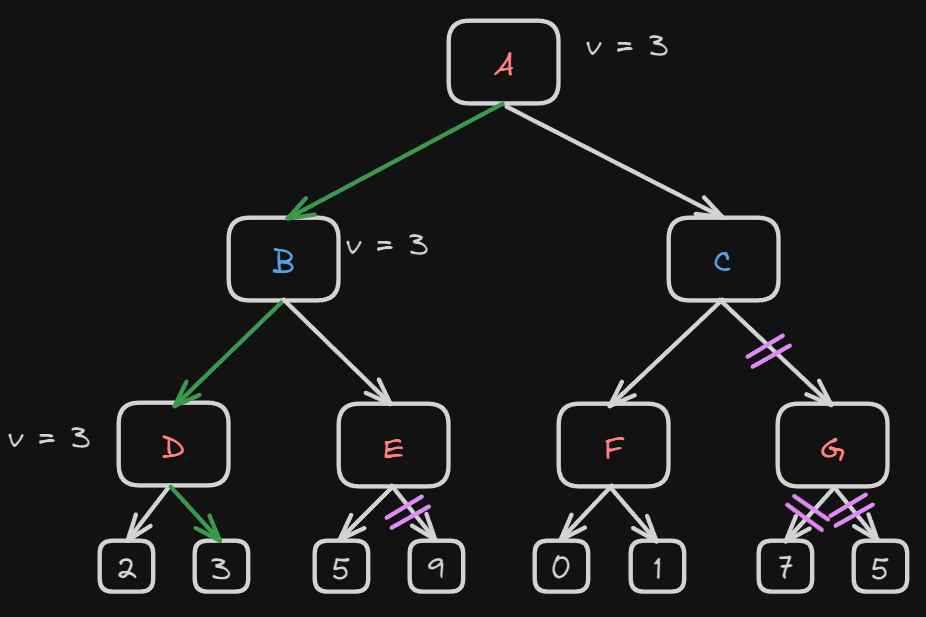
To implement this in code it’s super simple. All that is needed is to add the alpha and beta variables inside the minimax algorithm and simply check if the beta is less or equal to the alpha.
Here is the updated code:
def minimax(self, depth, alpha, beta, max_player):
score = self.evaluate()
if score is not None:
return score
if max_player:
max_value = -2
for i in range(3):
for j in range(3):
if self.board[i][j] == '-':
self.board[i][j] = 'O'
eval = self.minimax(depth + 1, alpha, beta, False)
self.board[i][j] = '-'
max_value = max(max_value, eval)
alpha = max(alpha, eval)
if beta <= alpha:
break
return max_value
else:
min_value = 2
for i in range(3):
for j in range(3):
if self.board[i][j] == '-':
self.board[i][j] = 'X'
eval = self.minimax(depth + 1,alpha, beta, True)
self.board[i][j] = "-"
min_value = min(min_value, eval)
beta = min(beta, eval)
if beta <= alpha:
break
return min_value
Here is the updated code for the best move method:
def best_move(self):
start_time = time.time()
best_score = float('-inf')
best_move = None
alpha = float('-inf')
beta = float('inf')
for i in range(3):
for j in range(3):
if self.board[i][j] == "-":
self.board[i][j] = "O"
move_score = self.minimax(0,alpha, beta, False)
self.board[i][j] = '-'
if move_score > best_score:
best_move = (i, j)
best_score = move_score
end_time = time.time()
execution_time = end_time - start_time
print(f"Minimax execution time: {execution_time:.6f} seconds")
return best_move
All that is new here is that we simply initialized alpha and beta.
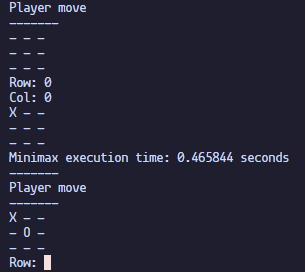
To test the effectiveness I timed the execution time of both the naive minimax and the minimax with alpha-beta pruning and here are the results.
Naive minimax execution time:
Minimax with alpha-beta pruning execution time:
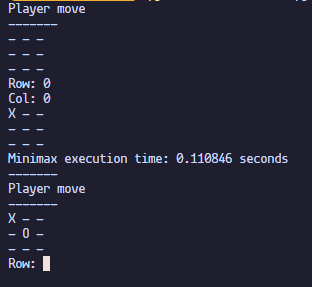
As you can see there is a noticeable execution time difference. Although alfa-beta pruning performs reasonably well for this example, this doesn’t mean that it’s this magical silver bullet that can decrease the execution time all the time.
In fact without alpha-beta pruning in some cases has the same performance of minimax. Minimax has a complexity of $O(b^d)$ where b is the number of branches and d is the depth of these branches. Now, implementing alfa beta pruning can yield a better result, $O(\sqrt(b^d))$ pruning a branch is not guaranteed. This means that even with alpha-beta pruning the algorithm can again perform as $O(b^d)$.
Complete code
import time
class TicTacToe:
def __init__(self) -> None:
self.board = [
['-', '-', '-'],
['-', '-', '-'],
['-', '-', '-']
]
'''
Display the board
'''
def display_board(self):
for i in range(3):
for j in range(3):
print(self.board[i][j], end=' ')
print()
'''
Human player makes a move
:param player: X or O
:return: row, col
'''
def human_play(self, player):
while True:
row = int(input("Row: "))
col = int(input("Col: "))
if row < 0 or row > 2 or col < 0 or col > 2:
print("Wrong row or col")
elif self.board[row][col] == '-':
self.board[row][col] = player
return row, col
else:
print("Error, position is occupied")
'''.
Check if there is a winner
:param player: X or O
:return: True or False
'''
def is_winner(self, player):
for i in range(3):
if all(self.board[i][j] == player for j in range(3)) or all(self.board[j][i] == player for j in range(3)):
return True
if all(self.board[i][i] == player for i in range(3)) or all(self.board[i][2 - i] == player for i in range(3)):
return True
return False
'''
Check if the board is full
:return: True or False
'''
def is_board_full(self):
for i in range(3):
for j in range(3):
if self.board[i][j] == '-':
return False
return True
'''
Evaluate the board
:return: 1 if O wins, -1 if X wins, 0 if it's a tie
'''
def evaluate(self):
if self.is_winner("O"):
return 1
elif self.is_winner("X"):
return -1
elif self.is_board_full():
return 0
else:
return None
'''
Minimax algorithm
:param depth: depth of the tree
:param alpha: alpha value
:param beta: beta value
:param max_player: True if it's the max player, False if it's the min player
:return:
'''
def minimax(self, depth, alpha, beta, max_player):
score = self.evaluate()
if score is not None:
return score
if max_player:
max_value = -2
for i in range(3):
for j in range(3):
if self.board[i][j] == '-':
self.board[i][j] = 'O'
eval = self.minimax(depth + 1, alpha, beta, False)
self.board[i][j] = '-'
max_value = max(max_value, eval)
alpha = max(alpha, eval)
if beta <= alpha:
break
return max_value
else:
min_value = 2
for i in range(3):
for j in range(3):
if self.board[i][j] == '-':
self.board[i][j] = 'X'
eval = self.minimax(depth + 1,alpha, beta, True)
self.board[i][j] = "-"
min_value = min(min_value, eval)
beta = min(beta, eval)
if beta <= alpha:
break
return min_value
'''
Find the best move
:return: row, col
'''
def best_move(self):
start_time = time.time()
best_score = float('-inf')
best_move = None
alpha = float('-inf')
beta = float('inf')
for i in range(3):
for j in range(3):
if self.board[i][j] == "-":
self.board[i][j] = "O"
move_score = self.minimax(0,alpha, beta, False)
self.board[i][j] = '-'
if move_score > best_score:
best_move = (i, j)
best_score = move_score
end_time = time.time()
execution_time = end_time - start_time
print(f"Minimax execution time: {execution_time:.6f} seconds")
return best_move
'''
Computer player makes a move
'''
def ai_play(self):
row, col = self.best_move()
self.board[row][col] = 'O'
'''
Play the game
'''
def play_game(self):
while True:
print("Player move")
print("-------")
self.display_board()
row, col = self.human_play("X")
self.display_board()
if self.is_winner("X"):
print("You won")
break
if self.is_board_full():
print("It's a tie")
break
self.ai_play()
print("-------")
if self.is_winner("O"):
print("You lost")
break
if self.is_board_full():
print("It's a tie")
break
game = TicTacToe()
game.play_game()