Sudoku is a popular game often seen in newspapers and other places. For the uninitiated, Sudoku is a logic-based combinatorial number-placement puzzle. The objective is to fill a 9×9 grid with digits so that each column, each row, and each of the nine 3×3 subgrids that compose the grid (also called “boxes”, “blocks”, or “regions”) contain all of the digits from 1 to 9.

This is what it looks like:

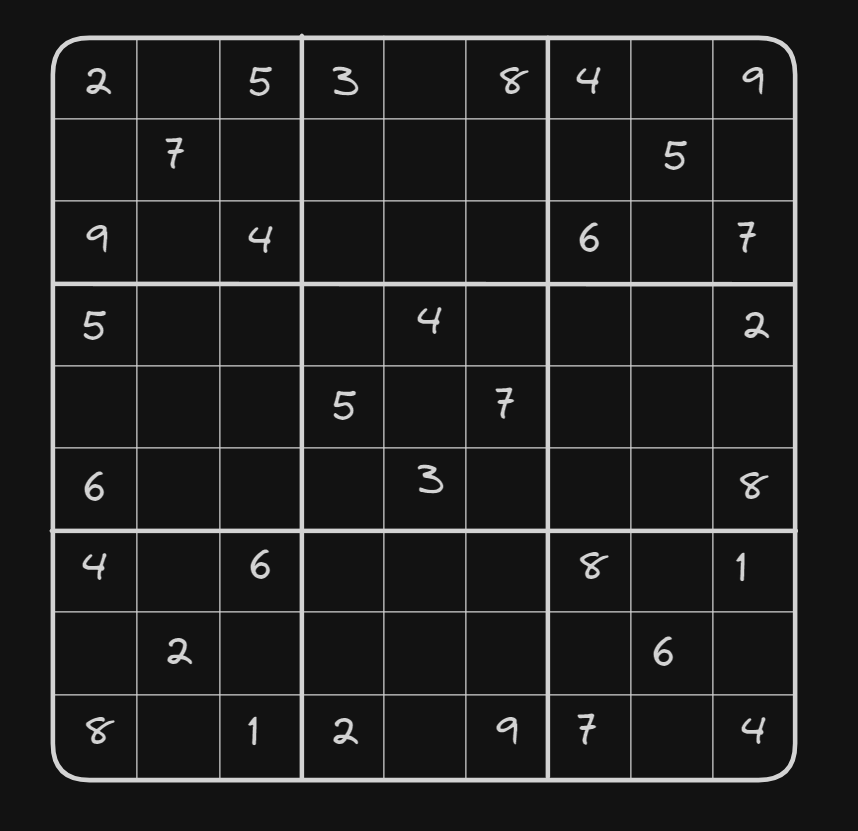
sudoku_board

The puzzle itself is fun but sometimes you just want to know the solution without having to solve the puzzle all by yourself. Luckily for us, we can make a simple program that can solve whatever sudoku we throw at it.

Backtracking

To solve this puzzle we will use an algorithm called backtracking. Backtracking is a brute-force algorithmic technique that systematically searches for a solution to a problem among all available options. When a solution is found to be incorrect or invalid, it backtracks to the previous step and tries another option until a valid solution is found or all possibilities are exhausted.

As far as algorithms are concerned this is a pretty simple one. The only thing that might make it a bit challenging to understand is the recursion but we will take a closer view when explaining the code implementation.

Code implementation

Before we can start implementing the backtracking algorithm we first need to implement a helper function called is_valid_move. As the name implies this function checks if that specific move is valid.

Check for move validity

def is_valid_move(board, row, col, number):

    corner_row = row - row % 3
    corner_col= col - col % 3

    for i in range(9):
        if board[row][i] == number:
            return False
        if board[i][col] == number:
            return False

        
    for i in range(3):
        for j in range(3):
            if board[corner_row + i][corner_col + j] == number:
                return False
    return True

This functions as input takes 4 arguments:

  • board which is the actual sudoku board
  • row which specifies the row where we are going to check our move
  • col which specifies the column where we are going to check our move
  • number the actual number/ move that we are checking

What we first need to do is to check the row and the column for the cell that we are checking:

    for i in range(9):
        if board[row][i] == number:
            return False
        if board[i][col] == number:
            return False

We iterate using a for loop 9 times, and in the first if statement, we check if our number already exists inside the row of the board. In the second if we do the same thing but for the column. In both cases, if we find the number that we are trying to put in a row or a column then we know the move is not valid so we return False.

Now we have to check for the square, which is a bit trickier to do but still doable:

    corner_row = row - row % 3
    corner_col= col - col % 3

    for i in range(3):
        for j in range(3):
            if board[corner_row + i][corner_col + j] == number:
                return False
    return True

What we first need to do is find the corner row and the corner column:

To do that we perform this simple math operation:

    corner_row = row - row % 3
    corner_col= col - col % 3

We take the row number and subtract the modulo of that row number. Same thing for the corner column. NOTE: the modulo operation is the remainder of the division: For example $\frac{25}{7}$ is $3$ modulo $4$

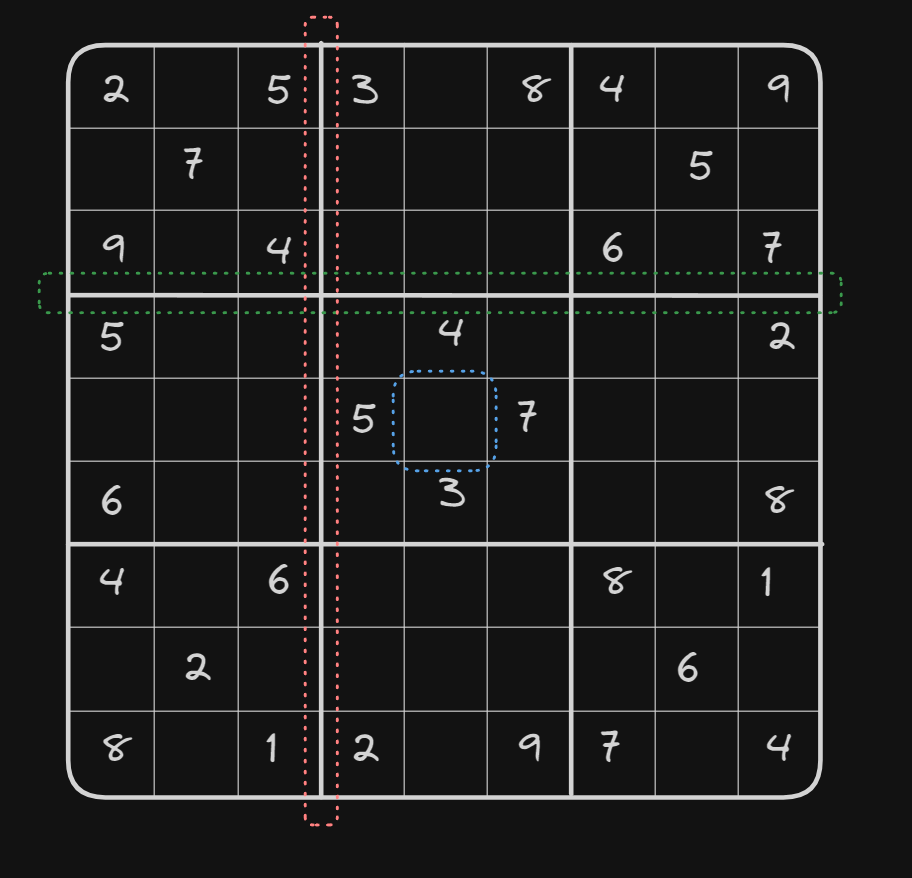
finding_the_box

If we want to place a move on the blue square, which is in a position [4][4] we can get the corner row by doing $4 - 1 = 3$, and to find the corner column we do the same operation $4 - 1 = 3$

    for i in range(3):
        for j in range(3):
            if board[corner_row + i][corner_col + j] == number:
                return False
    return True

Now, all we need to do is to check, based on the relative position of the corner_row and corner_col if that number exists inside the box.

check_inside_the_box

Backtracking implementation

Let’s take a look at the backtracking implementation:

def solve(board):
    for i in range(9):
        for j in range(9):
            if board[i][j] == 0:
                for n in range(1, 10):
                    if is_valid_move(board, i, j, n):
                        board[i][j] = n
                        solve(board)
                        board[i][j] = 0
                return 
    print_board(board)
    return

The first two loops are used to iterate inside the sudoku board. if the value is 0, which means it’s an empty cell, start by putting some values.

    for i in range(9):
        for j in range(9):
            if board[i][j] == 0:

    for n in range(1, 10):
        if is_valid_move(board, i, j, n):
            board[i][j] = n
            solve(board)
            board[i][j] = 0
    return

The for loop iterates over from 1 to 9 Then the function calls the is_valid_move if it’s true, place the number in the board.

At this point, we have decreased the possible cells by one. This is a good point to recursively call the solve function and then reset the cell value back to 0 (backtracking) to explore other possible solutions.

If no valid number n is found for the current cell, the function exits from the current recursive call, effectively backtracking to the previous cell.

    print_board(board)
    return

After all cells have been processed and filled with valid numbers, the function prints the solved Sudoku board using the print_board() function.

Let’s try to solve the sudoku given as the example:

Let’s copy the board and call the function:


sudoku_board = [[2, 0, 5, 3, 0, 8, 4, 0, 9],
                 [0, 7, 0, 0, 0, 0, 0, 5, 0],
                 [0, 0, 4, 0, 0, 0, 6, 0, 7],
                 [5, 0, 0, 0, 4, 0, 0, 0, 2],
                 [0, 0, 0, 5, 0, 7, 0, 0, 0],
                 [6, 0, 0, 0, 3, 0, 0, 0, 8],
                 [4, 0, 6, 0, 0, 0, 8, 0, 1],
                 [0, 2, 0, 0, 0, 0, 0, 6, 0],
                 [8, 0, 1, 2, 0, 9, 7, 0, 4]]

solve(sudoku_board)

When we run it we get these results:

[2, 6, 5, 3, 7, 8, 4, 1, 9]
[1, 7, 8, 4, 9, 6, 2, 5, 3]
[9, 3, 4, 1, 2, 5, 6, 8, 7]
[5, 8, 9, 6, 4, 1, 3, 7, 2]
[3, 4, 2, 5, 8, 7, 1, 9, 6]
[6, 1, 7, 9, 3, 2, 5, 4, 8]
[4, 9, 6, 7, 5, 3, 8, 2, 1]
[7, 2, 3, 8, 1, 4, 9, 6, 5]
[8, 5, 1, 2, 6, 9, 7, 3, 4]

Alternate solution

[2, 6, 5, 3, 7, 8, 4, 1, 9]
[9, 7, 8, 6, 1, 4, 2, 5, 3]
[1, 3, 4, 9, 2, 5, 6, 8, 7]
[5, 1, 7, 8, 4, 6, 3, 9, 2]
[3, 8, 2, 5, 9, 7, 1, 4, 6]
[6, 4, 9, 1, 3, 2, 5, 7, 8]
[4, 9, 6, 7, 5, 3, 8, 2, 1]
[7, 2, 3, 4, 8, 1, 9, 6, 5]
[8, 5, 1, 2, 6, 9, 7, 3, 4]

Alternate solution

[2, 6, 5, 3, 7, 8, 4, 1, 9]
[9, 7, 8, 6, 1, 4, 2, 5, 3]
[1, 3, 4, 9, 2, 5, 6, 8, 7]
[5, 1, 9, 8, 4, 6, 3, 7, 2]
[3, 8, 2, 5, 9, 7, 1, 4, 6]
[6, 4, 7, 1, 3, 2, 5, 9, 8]
[4, 9, 6, 7, 5, 3, 8, 2, 1]
[7, 2, 3, 4, 8, 1, 9, 6, 5]
[8, 5, 1, 2, 6, 9, 7, 3, 4]

Alternate solution

[2, 6, 5, 3, 7, 8, 4, 1, 9]
[9, 7, 8, 6, 1, 4, 2, 5, 3]
[3, 1, 4, 9, 2, 5, 6, 8, 7]
[5, 3, 7, 8, 4, 6, 1, 9, 2]
[1, 8, 2, 5, 9, 7, 3, 4, 6]
[6, 4, 9, 1, 3, 2, 5, 7, 8]
[4, 9, 6, 7, 5, 3, 8, 2, 1]
[7, 2, 3, 4, 8, 1, 9, 6, 5]
[8, 5, 1, 2, 6, 9, 7, 3, 4]

Alternate solution

[2, 6, 5, 3, 7, 8, 4, 1, 9]
[9, 7, 8, 6, 1, 4, 2, 5, 3]
[3, 1, 4, 9, 2, 5, 6, 8, 7]
[5, 3, 9, 8, 4, 6, 1, 7, 2]
[1, 8, 2, 5, 9, 7, 3, 4, 6]
[6, 4, 7, 1, 3, 2, 5, 9, 8]
[4, 9, 6, 7, 5, 3, 8, 2, 1]
[7, 2, 3, 4, 8, 1, 9, 6, 5]
[8, 5, 1, 2, 6, 9, 7, 3, 4]

Looks like the algorithm works!

NOTE: in this case, the sudoku had many solutions but for other sudoku, it may only have one possible solution.